It’s…it’s a histogram. – Dr. Grant

Okay. So maybe that isn’t the exact quote. But I think Dr. Grant would have been equally thrilled had he known the power of color histograms.

And more importantly, when the power goes out, the histograms don’t eat the tourists.

So, what exactly is a histogram? A histogram represents the distribution of colors in an image. It can be visualized as a graph (or plot) that gives a high-level intuition of the intensity (pixel value) distribution. We are going to assume a RGB color space in this example, so these pixel values will be in the range of 0 to 255. If you are working in a different color space, the pixel range may be different.

When plotting the histogram, the X-axis serves as our “bins”. If we construct a histogram with 256 bins, then we are effectively counting the number of times each pixel value occurs. In contrast, if we use only 2 (equally spaced) bins, then we are counting the number of times a pixel is in the range [0, 128) or [128, 255]. The number of pixels binned to the X-axis value is then plotted on the Y-axis.

Looking for the source code to this post?

Jump Right To The Downloads Section

OpenCV and Python versions:
This example will run on Python 2.7 and OpenCV 2.4.X/OpenCV 3.0+.

By simply examining the histogram of an image, you get a general understanding regarding the contrast, brightness, and intensity distribution.

This post will give you an OpenCV histogram example, from start to finish.

Application to Image Search Engines

In context of image search engines, histograms can serve as feature vectors (i.e. a list of numbers used to quantify an image and compare it to other images). In order to use color histograms in image search engines, we make the assumption that images with similar color distributions are semantically similar. I will talk more about this assumption in the “Drawbacks” section later in this post; however, for the time being, let’s go ahead and assume that images with similar color distributions have similar content.

Comparing the “similarity” of color histograms can be done using a distance metric. Common choices include: Euclidean, correlation, Chi-squared, intersection, and Bhattacharyya. In most cases, I tend to use the Chi-squared distance, but the choice is usually dependent on the image dataset being analyzed. No matter which distance metric you use, we’ll be using OpenCV to extract our color histograms.

Touring Jurassic Park

Let’s imagine that we were along with Dr. Grant and company on their first Jurassic Park tour. We brought along our cell phone to document the entire experience (and let’s also pretend that camera phones were a “thing” back then). Assuming we didn’t pull a Dennis Nedry a have our face eaten by a Dilophosaurus, we could later download the pictures from our smartphones to our computers and compute histograms for each of the images.

At the very beginning of the tour we spent a lot of times in the labs, learning about DNA and witnessing the hatching of a baby velociraptor. These labs have a lot of “steel” and “gray” colors to them. Later on, we got into our jeeps and drove into the park. The park itself is a jungle — lots of green colors.

So based on these two color distributions, which one do you think the Dr. Grant image above is more similar to?

Well, we see that there is a fair amount of greenery in the background of the photo. In all likelihood, the color distribution of the Dr. Grant photo would be more “similar” to our pictures taken during the jungle tour vs. our pictures taken in the lab.

Using OpenCV to Compute Histograms

Now, let’s start building some color histograms of our own.

We will be using the cv2.calcHist function in OpenCV to build our histograms. Before we get into any code examples, let’s quickly review the function:

cv2.calcHist(images, channels, mask, histSize, ranges)

1. images: This is the image that we want to compute a histogram for. Wrap it as a list: [myImage].
2. channels: A list of indexes, where we specify the index of the channel we want to compute a histogram for. To compute a histogram of a grayscale image, the list would be [0]. To compute a histogram for all three red, green, and blue channels, the channels list would be [0, 1, 2].
3. mask: I haven’t covered masking yet in this blog yet, but essentially, a mask is a uint8 image with the same shape as our original image, where pixels with a value of zero are ignored and pixels with a value greater than zero are included in the histogram computation. Using masks allow us to only compute a histogram for a particular region of an image. For now, we’ll just use a value of None for the mask.
4. histSize: This is the number of bins we want to use when computing a histogram. Again, this is a list, one for each channel we are computing a histogram for. The bin sizes do not all have to be the same. Here is an example of 32 bins for each channel: [32, 32, 32].
5. ranges: The range of possible pixel values. Normally, this is [0, 256] for each channel, but if you are using a color space other than RGB (such as HSV), the ranges might be different.

Now that we have an understanding of the cv2.calcHist function, let’s write some actual code.

# import the necessary packages
from matplotlib import pyplot as plt
import numpy as np
import argparse
import cv2

# construct the argument parser and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-i", "--image", required = True, help = "Path to the image")
args = vars(ap.parse_args())

# load the image and show it
image = cv2.imread(args["image"])
cv2.imshow("image", image)

This code isn’t very exciting yet. All we are doing is importing the packages we will need, setting up an argument parser, and loading our image.

# convert the image to grayscale and create a histogram
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
cv2.imshow("gray", gray)
hist = cv2.calcHist([gray], [0], None, [256], [0, 256])
plt.figure()
plt.title("Grayscale Histogram")
plt.xlabel("Bins")
plt.ylabel("# of Pixels")
plt.plot(hist)
plt.xlim([0, 256])

Now things are getting a little more interesting. On line 2, we convert the image from the RGB colorspace to grayscale. Line 4 computes the actual histogram. Go ahead and match the arguments of the code up with the function documentation above. We can see that our first parameter is the grayscale image. A grayscale image has only one channel, hence we a use value of [0] for channels. We don’t have a mask, so we set the mask value to None. We will use 256 bins in our histogram, and the possible values range from 0 to 256.

A call to plt.show() displays:

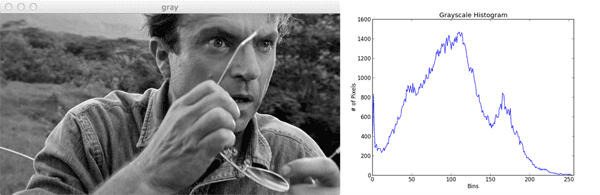
Not bad. How do we interpret this histogram? Well, the bins (0-255) are plotted on the X-axis. And the Y-axis counts the number of pixels in each bin. The majority of pixels fall in the range of ~50 to ~125. Looking at the right tail of the histogram, we see very few pixels in the range 200 to 255. This means that there are very few “white” pixels in the image.

Now that we’ve seen at a grayscale histogram, let’s look at what I call a “flattened” color histogram:

# grab the image channels, initialize the tuple of colors,
# the figure and the flattened feature vector
chans = cv2.split(image)
colors = ("b", "g", "r")
plt.figure()
plt.title("'Flattened' Color Histogram")
plt.xlabel("Bins")
plt.ylabel("# of Pixels")
features = []

# loop over the image channels
for (chan, color) in zip(chans, colors):
	# create a histogram for the current channel and
	# concatenate the resulting histograms for each
	# channel
	hist = cv2.calcHist([chan], [0], None, [256], [0, 256])
	features.extend(hist)

	# plot the histogram
	plt.plot(hist, color = color)
	plt.xlim([0, 256])

# here we are simply showing the dimensionality of the
# flattened color histogram 256 bins for each channel
# x 3 channels = 768 total values -- in practice, we would
# normally not use 256 bins for each channel, a choice
# between 32-96 bins are normally used, but this tends
# to be application dependent
print "flattened feature vector size: %d" % (np.array(features).flatten().shape)

There’s definitely more code involved in computing a flattened color histogram vs. a grayscale histogram. Let’s tear this code apart and get a better handle on what’s going on:

• Lines 29 and 30: The first thing we are going to do is split the image into its three channels: blue, green, and red. Normally, we read this is a red, green, blue (RGB). However, OpenCV stores the image as a NumPy array in reverse order: BGR. This is important to note. We then initialize a tuple of strings representing the colors.
• Lines 31-35: Here we are just setting up our PyPlot figure and initializing our list of concatenated histograms.
• Line 38: Let’s start looping over the channels.
• Line 42 and 43: We are now computing a histogram for each channel. Essentially, this is the same as computing a histogram for a single channeled grayscale image. We then concatenate the color histogram to our features list.
• Lines 46 and 47: Plot the histogram using the current channel name.
• Line 55: Here we are just examining the shape of our flattened color histogram. I call this a “flattened” histogram not because the (1) histogram has zero “peaks” or (2) I am calling NumPy’s flatten() method. I call this a “flattened” histogram because the histogram is a single list of pixel counts. Later, we explore multi-dimensional histograms (2D and 3D). A flattened histogram is simply the histogram for each individual channel concatenated together.

Now let’s plot our color histograms:

Awesome. That was pretty simple. What does this histogram tell us? Well, there is a peak in the dark blue pixel values around bin #50. This range of blue refers to Grant’s blue shirt. And the much larger range of green pixels from bin #50 to #125 refers to the forest behind Dr. Grant in the background.

Multi-dimensional Histograms

Up until this point, we have computed a histogram for only one channel at a time. Now we move on to multi-dimensional histograms and take into consideration two channels at a time.

The way I like to explain multi-dimensional histograms is to use the word AND. For example, we can ask a question such as
“how many pixels have a Red value of 10 AND a Blue value of 30?” How many pixels have a Green value of 200 AND a Red value of 130? By using the conjunctive AND we are able to construct multi-dimensional histograms.

It’s that simple. Let’s checkout some code to automate the process of building a 2D histogram:

# let's move on to 2D histograms -- I am reducing the
# number of bins in the histogram from 256 to 32 so we
# can better visualize the results
fig = plt.figure()

# plot a 2D color histogram for green and blue
ax = fig.add_subplot(131)
hist = cv2.calcHist([chans[1], chans[0]], [0, 1], None,
	[32, 32], [0, 256, 0, 256])
p = ax.imshow(hist, interpolation = "nearest")
ax.set_title("2D Color Histogram for Green and Blue")
plt.colorbar(p)

# plot a 2D color histogram for green and red
ax = fig.add_subplot(132)
hist = cv2.calcHist([chans[1], chans[2]], [0, 1], None,
	[32, 32], [0, 256, 0, 256])
p = ax.imshow(hist, interpolation = "nearest")
ax.set_title("2D Color Histogram for Green and Red")
plt.colorbar(p)

# plot a 2D color histogram for blue and red
ax = fig.add_subplot(133)
hist = cv2.calcHist([chans[0], chans[2]], [0, 1], None,
	[32, 32], [0, 256, 0, 256])
p = ax.imshow(hist, interpolation = "nearest")
ax.set_title("2D Color Histogram for Blue and Red")
plt.colorbar(p)

# finally, let's examine the dimensionality of one of
# the 2D histograms
print "2D histogram shape: %s, with %d values" % (
	hist.shape, hist.flatten().shape[0])

Yes, this is a fair amount of code. But that’s only because we are computing a 2D color histogram for each combination of RGB channels: Red and Green, Red and Blue, and Green and Blue.

Now that we are working with multi-dimensional histograms, we need to keep in mind the number of bins we are using. In previous examples, I’ve used 256 bins for demonstration purposes. However, if we used a 256 bins for each dimension in a 2D histogram, our resulting histogram would have 65,536 separate pixel counts. Not only is this wasteful of resources, it’s not practical. Most applications using somewhere between 8 and 64 bins when computing multi-dimensional histograms. As Lines 64 and 65 show, I am now using 32 bins instead of 256.

The most important take away from this code can be seen by inspecting the first arguments to the cv2.calcHist function. Here we see that we are passing in a list of two channels: the Green and Blue channels. And that’s all there is to it.

So how is a 2D histogram stored in OpenCV? It’s a 2D NumPy array. Since I used 32 bins for each channel, I now have a 32×32 histogram. We can treat this histogram as a feature vector simply by flattening it (Lines 88 and 89). Flattening our histograms yields a list with 1024 values.

How do we visualize a 2D histogram? Let’s take a look.

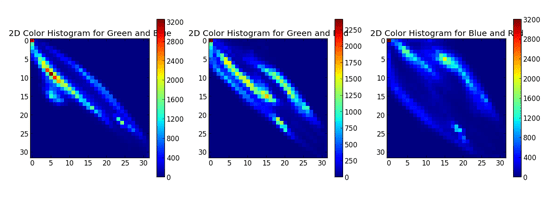
In the above Figure, we see three graphs. The first is a 2D color histogram for the Green and Blue channels, the second for Green and Red, and the third for Blue and Red. Shades of blue represent low pixel counts, whereas shades of red represent large pixel counts (i.e. peaks in the 2D histogram). We can see such a peak in the Green and Blue 2D histogram (the first graph) when X=5 and Y=10.

Using a 2D histogram takes into account two channels at a time. But what if we wanted to account for all three RGB channels? You guessed it. We’re now going to build a 3D histogram.

# our 2D histogram could only take into account 2 out
# of the 3 channels in the image so now let's build a
# 3D color histogram (utilizing all channels) with 8 bins
# in each direction -- we can't plot the 3D histogram, but
# the theory is exactly like that of a 2D histogram, so
# we'll just show the shape of the histogram
hist = cv2.calcHist([image], [0, 1, 2],
	None, [8, 8, 8], [0, 256, 0, 256, 0, 256])
print "3D histogram shape: %s, with %d values" % (
	hist.shape, hist.flatten().shape[0])

The code here is very simple — it’s just an extension from the code above. We are now computing an 8x8x8 histogram for each of the RGB channels. We can’t visualize this histogram, but we can see that the shape is indeed (8, 8, 8) with 512 values. Again, treating the 3D histogram as a feature vector can be done by simply flattening the array.

Color Spaces

The examples in this post have only explored the RGB color space, but histograms can be constructed for any color space in OpenCV. Discussing color spaces is outside the context of this post, but if you are interested, check out the documentation on converting color spaces.

Drawbacks

Earlier in this post we made the assumption that images with similar color distributions are semantically similar. For small, simple datasets, this may in fact be true. However, in practice, this assumption does not always hold.

Let’s think about why this for.

For one, color histograms, by definition ignore both the shape and texture of the object(s) in the image. This means that color histograms have no concept of the shape of an object or the texture of the object. Furthermore, histograms also disregard any spatial information (i.e. where in the image the pixel value came from). An extension to the histogram, the color correlogram, can be used to encode a spatial relationship amongst pixels.

Let’s think about Chic Engine, my visual fashion search engine iPhone app. I have different categories for different types of clothes, such as shoes and shirts. If I were using color histograms to describe a red shoe and a red shirt, the histogram would assume they were the same object. Clearly they are both red, but the semantics end there — they are simply not the same. Color histograms simply have no way to “model” what a shoe or a shirt is.

Finally, color histograms are sensitive to “noise”, such as changes in lighting in the environment the image was captured under and quantization errors (selecting which bin to increment). Some of these limitations can potentially be mitigated by using a different color space than RGB (such as HSV or L*a*b*).

However, all that said, histograms are still widely used as image descriptors. They are dead simple to implement and very fast to compute. And while they have their limitations, they are very powerful when used correctly and in the right context.

What's next? I recommend PyImageSearch University.

Course information:
30+ total classes • 39h 44m video • Last updated: 12/2021
★★★★★ 4.84 (128 Ratings) • 3,000+ Students Enrolled

I strongly believe that if you had the right teacher you could master computer vision and deep learning.

Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?

That’s not the case.

All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.

If you're serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.

Inside PyImageSearch University you'll find:

• ✓ 30+ courses on essential computer vision, deep learning, and OpenCV topics
• ✓ 30+ Certificates of Completion
• ✓ 39h 44m on-demand video
• ✓ Brand new courses released every month, ensuring you can keep up with state-of-the-art techniques
• ✓ Pre-configured Jupyter Notebooks in Google Colab
• ✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
• ✓ Access to centralized code repos for all 500+ tutorials on PyImageSearch
• ✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
• ✓ Access on mobile, laptop, desktop, etc.

Click here to join PyImageSearch University

Until Monday!

Download the Source Code and FREE 17-page Resource Guide

Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you'll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!

Download the code!

Website