In this tutorial, you will learn how to implement face recognition using the Eigenfaces algorithm, OpenCV, and scikit-learn.

Our previous tutorial introduced the concept of face recognition — detecting the presence of a face in an image/video and then subsequently identifying the face.
We’re now going to learn how to utilize linear algebra, and more specifically, principal component analysis, to recognize faces.
This algorithm is important to understand from both a theoretical and historical perspective, so make sure you fully read the guide and digest it.
To learn how to implement Eigenfaces for face recognition, just keep reading.
OpenCV Eigenfaces for Face Recognition
In the first part of this tutorial, we’ll discuss the Eigenfaces algorithm, including how it utilizes linear algebra and Principal Component Analysis (PCA) to perform face recognition.
From there we’ll configure our development environment and then review our project directory structure.
I’ll then show you how to implement Eigenfaces for face recognition using OpenCV and scikit-learn.
Let’s get started!
Eigenfaces, Principal Component Analysis (PCA), and face recognition
Fundamentals of the Eigenfaces algorithm were first presented by Sirovich and Kirby in their 1987 paper, Low-Dimensional Procedure for the Characterization of Human Faces, and then later formalized by Turk and Pentland in their 1991 CVPR paper, Face Recognition Using Eigenfaces.
These papers are considered to be a seminal work in the history of computer vision — and while other approaches have since been proposed that can outperform Eigenfaces, it’s still important that we take the time to understand and appreciate this algorithm. We’ll be discussing the technical inner workings of Eigenfaces here today.
The first step in the Eigenfaces algorithm is to input a dataset of N face images:

For face recognition to be successful (and somewhat robust), we should ensure we have multiple images per person we want to recognize.
Let’s now consider an image containing a face:

When applying Eigenfaces, each face is represented as a grayscale, K×K bitmap of pixels (images do not have to be square, but for the sake of this example, it’s easier to explain if we assume square images).
In order to apply the Eigenfaces algorithm, we need to form a single vector from the image. This is accomplished by “flattening” each image into a 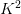

Again, all we have done here is taken a K×K image and concatenated all of the rows together, forming a single, long 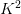
After each image in the dataset has been flattened, we form a matrix of flattened images like this, where Z is the total number of images in our dataset:

Our entire dataset is now contained in a single matrix, M.
Given this matrix M, we are now ready to apply Principal Component Analysis (PCA), the cornerstone of the Eigenfaces algorithm.
A complete review associated with the linear algebra underlying PCA is outside the scope of this lesson (for a detailed review of the algorithm, please see Andrew Ng’s discussion on the topic), but the general outline of the algorithm follows:
- Compute the mean
of each column in the matrix, giving us the average pixel intensity value for every (x, y)-coordinate in the image dataset.
- Subtract the
from each column
— this is called mean centering the data and is a required step when performing PCA.
- Now that our matrix M has been mean centered, compute the covariance matrix.
- Perform an eigenvalue decomposition on the covariance matrix to get the eigenvalues
and eigenvectors
.
- Sort
by
, largest to smallest.
- Take the top N eigenvectors with the largest corresponding eigenvalue magnitude.
- Transform the input data by projecting (i.e., taking the dot product) it onto the space created by the top N eigenvectors — these eigenvectors are called our eigenfaces.
Again, a complete review on manually computing the covariance matrix and performing an eigenvalue decomposition is outside the scope of this lesson. For a more detailed review, please see Andrew Ng’s machine learning lessons or consult this excellent Principal Components Analysis primer by Lindsay Smith.
However, before we perform actual face identification using the Eigenfaces algorithm, let’s actually discuss these eigenface representations:

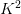 .
.Each row in the matrix above is an eigenface with 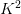
What does this mean? Well, since each of these eigenface representations is actually a 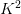

The image on the left is simply the average of all faces in our dataset, while the figures on the right show the most prominent deviations from the mean in our face dataset.
This can be thought of as a visualization of the dimension in which people’s faces vary the most. Lighter regions correspond to higher variation, where darker regions correspond to little to no variation. Here, we can see that our eigenface representation captures considerable variance in the eyes, hair, nose, lips, and cheek structure.
Now that we understand how the Eigenfaces representation is constructed, let’s move on to learning how we can actually identify faces using Eigenfaces.
Identifying faces using Eigenfaces
Given our eigenface vectors, we can represent a new face by taking the dot product between the (flattened) input face image and the N eigenfaces. This allows us to represent each face as a linear combination of principal components:
Query Face = 36% of Eigenface #1 + -8% of Eigenface #2 + … + 21% of Eigenface N
To perform the actual face identification, Sirovich and Kirby proposed taking the Euclidean distance between projected eigenface representations — this is, in essence, a k-NN classifier:

The smaller the Euclidean distance (denoted as the function, d), the more “similar” the two faces are — the overall identification is found by taking the label associated with the face with the smallest Euclidean distance.
For example, in Figure 7 the top image pair has a distance of 0 because the two faces are identical (i.e., the same image).
The middle image pair has a distance of 0.07 — while the images are different they contain the same face.
The third image pair has a much larger distance (9.81), indicating that the two faces presented to the Eigenfaces algorithm are not the same person.
In practice, we often don’t rely on a simple k-NN algorithm for identification. Accuracy can be increased by using more advanced machine learning algorithms, such as Support Vector Machines (SVMs), Random Forests, etc. The implementation covered here today will utilize SVMs.
Configuring your development environment
To learn how to use the Eigenfaces algorithm for face recognition, you need to have OpenCV, scikit-image, and scikit-learn installed on your machine:
Luckily, OpenCV is pip-installable:
$ pip install opencv-contrib-python $ pip install scikit-image $ pip install scikit-learn
If you need help configuring your development environment for OpenCV, I highly recommend that you read my pip install OpenCV guide — it will have you up and running in a matter of minutes.
Having problems configuring your development environment?

All that said, are you:
- Short on time?
- Learning on your employer’s administratively locked system?
- Wanting to skip the hassle of fighting with the command line, package managers, and virtual environments?
- Ready to run the code right now on your Windows, macOS, or Linux systems?
Then join PyImageSearch University today!
Gain access to Jupyter Notebooks for this tutorial and other PyImageSearch guides that are pre-configured to run on Google Colab’s ecosystem right in your web browser! No installation required.
And best of all, these Jupyter Notebooks will run on Windows, macOS, and Linux!
The CALTECH Faces dataset

The CALTECH Faces challenge is a benchmark dataset for face recognition algorithms. Overall, the dataset consists of 450 images of approximately 27 unique people. Each subject was captured under various lighting conditions, background scenes, and facial expressions, as seen in Figure 9.
The overall goal of this tutorial is to apply the Eigenfaces face recognition algorithm to identify each of the subjects in the CALTECH Faces dataset.
Note: I’ve included a slightly modified version of the CALTECH Faces dataset in the “Downloads” associated with this tutorial. The slightly modified version includes an easier to parse directory structure with faux names assigned to each of the subjects, making it easier to evaluate the accuracy of our face recognition system. Again, you do not need to download the CALTECH Faces dataset from CALTECH’s servers — just use the “Downloads” associated with this guide.
Project structure
Before we can implement Eigenfaces with OpenCV, let’s first review our project directory structure.
Be sure to access the “Downloads” section of this tutorial to retrieve the source code, pre-trained face detector model, and CALTECH faces dataset.
After unarchiving the .zip you should have the following structure:
$ tree --dirsfirst --filelimit 20 . ├── caltech_faces [26 entries exceeds filelimit, not opening dir] ├── face_detector │ ├── deploy.prototxt │ └── res10_300x300_ssd_iter_140000.caffemodel ├── pyimagesearch │ ├── __init__.py │ └── faces.py └── eigenfaces.py 4 directories, 7 files
Our project directory structure is essentially identical to that of last week when we discussed implementing face recognition with Local Binary Patterns (LBPs):
face_detector: Stores OpenCV’s pre-trained deep learning-based face detectorpyimagesearch: Contains thedetect_facesandload_face_datasethelper functions which perform face detection and load our CALTECH Faces dataset from disk, respectivelyeigenfaces.py: Our driver script that trains the Eigenfaces model
The caltech_faces directory is structured as follows:
$ ls -l caltech_faces/ abraham alberta allen carmen conrad cynthia darrell flyod frank glen gloria jacques judy julie kathleen kenneth lewis mae phil raymond rick ronald sherry tiffany willie winston $ ls -l caltech_faces/abraham/*.jpg caltech_faces/abraham/image_0022.jpg caltech_faces/abraham/image_0023.jpg caltech_faces/abraham/image_0024.jpg ... caltech_faces/abraham/image_0041.jpg
Inside this directory is a subdirectory containing images for each of the people we want to recognize. As you can see, we have multiple images for each person we want to recognize. These images will serve as our training data such that our LBP face recognizer can learn what each individual looks like.
Implementing face detection and CALTECH face dataset loading
In this section, we’ll be implementing two functions that will facilitate working with the CALTECH Faces dataset:
detect_faces: Accepts an input image and performs face detection, returning the bounding box (x, y)-coordinates of all faces in the imageload_face_dataset: Loops over all images in the CALTECH Faces dataset, performs face detection, and returns both the face ROIs and class labels (i.e., names of the individuals) to the calling function
Both of these functions were covered in detail in last week’s tutorial on Face Recognition with Local Binary Patterns (LBPs) and OpenCV. I’ve included both of these functions here today as a matter of completeness, but you should refer to the previous article for more details on them.
With that said, open faces.py inside the pyimagesearch module and let’s take a peek at what’s going on:
# import the necessary packages
from imutils import paths
import numpy as np
import cv2
import os
def detect_faces(net, image, minConfidence=0.5):
# grab the dimensions of the image and then construct a blob
# from it
(h, w) = image.shape[:2]
blob = cv2.dnn.blobFromImage(image, 1.0, (300, 300),
(104.0, 177.0, 123.0))
# pass the blob through the network to obtain the face detections,
# then initialize a list to store the predicted bounding boxes
net.setInput(blob)
detections = net.forward()
boxes = []
# loop over the detections
for i in range(0, detections.shape[2]):
# extract the confidence (i.e., probability) associated with
# the detection
confidence = detections[0, 0, i, 2]
# filter out weak detections by ensuring the confidence is
# greater than the minimum confidence
if confidence > minConfidence:
# compute the (x, y)-coordinates of the bounding box for
# the object
box = detections[0, 0, i, 3:7] * np.array([w, h, w, h])
(startX, startY, endX, endY) = box.astype("int")
# update our bounding box results list
boxes.append((startX, startY, endX, endY))
# return the face detection bounding boxes
return boxes
The detect_faces function accepts our input face detector net, an input image to apply face detection to, and the minConfidence used to filter out weak/false-positive detections.
We then preprocess the input image such that we can pass it through the face detection model (Lines 11 and 12). This function performs resizing, scaling, and mean subtraction.
Lines 16 and 17 perform face detection, resulting in a detections list which we loop over on Line 21.
Provided the confidence of the detected face is greater than the minConfidence, we extract the bounding box coordinates and update our boxes list.
The boxes list is then returned to the calling function.
Our second function load_face_dataset, loops over all images in the CALTECH Faces dataset and applies face detection to each image:
def load_face_dataset(inputPath, net, minConfidence=0.5, minSamples=15): # grab the paths to all images in our input directory, extract # the name of the person (i.e., class label) from the directory # structure, and count the number of example images we have per # face imagePaths = list(paths.list_images(inputPath)) names = [p.split(os.path.sep)[-2] for p in imagePaths] (names, counts) = np.unique(names, return_counts=True) names = names.tolist() # initialize lists to store our extracted faces and associated # labels faces = [] labels = [] # loop over the image paths for imagePath in imagePaths: # load the image from disk and extract the name of the person # from the subdirectory structure image = cv2.imread(imagePath) name = imagePath.split(os.path.sep)[-2] # only process images that have a sufficient number of # examples belonging to the class if counts[names.index(name)] < minSamples: continue
The load_face_dataset requires that we supply the inputPath to the CALTECH Faces dataset, the face detection model (net), the minimum confidence for a positive detection, and the minimum number of example images required for each face.
Line 46 grabs the paths to all input images in the CALTECH Faces dataset while Lines 47-49 extract the names of the individuals from the subdirectory structure, and counts the number of images associated with each person.
We then loop over all imagePaths on Line 57, loading the image from disk and extracting the name of the person.
If there are less than minSamples images for this particular name, we throw out the image and will not consider that individual when training our face recognizer. We do this to avoid class imbalance issues (handling class imbalance is outside the scope of this tutorial).
Provided the minSamples test passes we then move on to performing face detection:
# perform face detection boxes = detect_faces(net, image, minConfidence) # loop over the bounding boxes for (startX, startY, endX, endY) in boxes: # extract the face ROI, resize it, and convert it to # grayscale faceROI = image[startY:endY, startX:endX] faceROI = cv2.resize(faceROI, (47, 62)) faceROI = cv2.cvtColor(faceROI, cv2.COLOR_BGR2GRAY) # update our faces and labels lists faces.append(faceROI) labels.append(name) # convert our faces and labels lists to NumPy arrays faces = np.array(faces) labels = np.array(labels) # return a 2-tuple of the faces and labels return (faces, labels)
For each detected face we extract the face ROI, resize it to a fixed size (a requirement when performing PCA), and then convert the image from color to grayscale.
The resulting set of faces and labels are returned to the calling function.
Note: If you would like more details on how both these functions work, I suggest you read my previous guide on Face Recognition with Local Binary Patterns (LBPs) and OpenCV, where I cover both detect_faces and load_face_dataset in detail.
Implementing Eigenfaces with OpenCV
Let’s now implement Eigenfaces for face recognition with OpenCV!
Open the eigenfaces.py file in your project directory structure and let’s get coding:
# import the necessary packages from sklearn.preprocessing import LabelEncoder from sklearn.decomposition import PCA from sklearn.svm import SVC from sklearn.model_selection import train_test_split from sklearn.metrics import classification_report from skimage.exposure import rescale_intensity from pyimagesearch.faces import load_face_dataset from imutils import build_montages import numpy as np import argparse import imutils import time import cv2 import os
Lines 2-15 import our required Python packages. Our notable imports include:
LabelEncoder: Used to encode the class labels (i.e., names of the individuals) as integers rather than strings (this is a requirement in order to utilize OpenCV’s LBP face recognizer)PCA: Performs Principal Component AnalysisSVC: Our Support Vector Machine (SVM) classifier which we’ll train on top of the eigenface representation of our datasettrain_test_split: Constructs a training and testing split from our CALTECH Faces datasetrescale_intensity: Used to visualize the eigenface representations
We can now move on to command line arguments:
# construct the argument parser and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-i", "--input", type=str, required=True,
help="path to input directory of images")
ap.add_argument("-f", "--face", type=str,
default="face_detector",
help="path to face detector model directory")
ap.add_argument("-c", "--confidence", type=float, default=0.5,
help="minimum probability to filter weak detections")
ap.add_argument("-n", "--num-components", type=int, default=150,
help="# of principal components")
ap.add_argument("-v", "--visualize", type=int, default=-1,
help="whether or not PCA components should be visualized")
args = vars(ap.parse_args())
Our command line arguments include:
--input: The path to our input dataset containing images of the individuals we want to train our LBP face recognizer on--face: Path to our OpenCV deep learning face detector--confidence: Minimum probability used to filter out weak detections--num-components: The number of principal components when applying PCA (we’ll be discussing this variable in more detail shortly)--visualize: Whether or not to visualize the Eigenfaces representation of the data
Next, let’s load our face detection model from disk:
# load our serialized face detector model from disk
print("[INFO] loading face detector model...")
prototxtPath = os.path.sep.join([args["face"], "deploy.prototxt"])
weightsPath = os.path.sep.join([args["face"],
"res10_300x300_ssd_iter_140000.caffemodel"])
net = cv2.dnn.readNet(prototxtPath, weightsPath)
And from there, let’s load the CALTECH Faces dataset:
# load the CALTECH faces dataset
print("[INFO] loading dataset...")
(faces, labels) = load_face_dataset(args["input"], net,
minConfidence=0.5, minSamples=20)
print("[INFO] {} images in dataset".format(len(faces)))
# flatten all 2D faces into a 1D list of pixel intensities
pcaFaces = np.array([f.flatten() for f in faces])
# encode the string labels as integers
le = LabelEncoder()
labels = le.fit_transform(labels)
# construct our training and testing split
split = train_test_split(faces, pcaFaces, labels, test_size=0.25,
stratify=labels, random_state=42)
(origTrain, origTest, trainX, testX, trainY, testY) = split
Lines 41 and 42 load the CALTECH Faces dataset from disk, resulting a 2-tuple:
faces: Face ROIs from the CALTECH Faces datasetlabels: The name of the individual in each face ROI
Keep in mind that each face is a 2D, M×N image; however, in order to apply PCA, we need a 1D representation of each face. Therefore, Line 46 flattens all 2D faces into a 1D list of pixel intensities.
We then encode the labels as integers rather than strings.
Lines 53-55 then construct our training and testing split, using 75% of the data for training and the remaining 25% for evaluation.
Let’s now perform PCA on our 1D lists of faces:
# compute the PCA (eigenfaces) representation of the data, then
# project the training data onto the eigenfaces subspace
print("[INFO] creating eigenfaces...")
pca = PCA(
svd_solver="randomized",
n_components=args["num_components"],
whiten=True)
start = time.time()
trainX = pca.fit_transform(trainX)
end = time.time()
print("[INFO] computing eigenfaces took {:.4f} seconds".format(
end - start))
Here, we indicate N, the number of principal components we are going to use when initializing the PCA class. After we have found the top --num-components, we then use them to project the original training data to the Eigenface subspace.
Now that we’ve performed PCA, let’s visualize the top components:
# check to see if the PCA components should be visualized
if args["visualize"] > 0:
# initialize the list of images in the montage
images = []
# loop over the first 16 individual components
for (i, component) in enumerate(pca.components_[:16]):
# reshape the component to a 2D matrix, then convert the data
# type to an unsigned 8-bit integer so it can be displayed
# with OpenCV
component = component.reshape((62, 47))
component = rescale_intensity(component, out_range=(0, 255))
component = np.dstack([component.astype("uint8")] * 3)
images.append(component)
# construct the montage for the images
montage = build_montages(images, (47, 62), (4, 4))[0]
# show the mean and principal component visualizations
# show the mean image
mean = pca.mean_.reshape((62, 47))
mean = rescale_intensity(mean, out_range=(0, 255)).astype("uint8")
cv2.imshow("Mean", mean)
cv2.imshow("Components", montage)
cv2.waitKey(0)
Line 71 makes a check to see if the --visualize command line argument is set, and if so, we initialize a list of images to store our visualizations.
From there, we loop over each of the top PCA components (Line 76), reshape the image into a 47×62 pixel bitmap image (Line 80), and then rescale the pixel intensities to the range [0, 255] (Line 81).
Why do we bother with the rescaling operation?
Simple — our eigenvalue decomposition results in real-valued feature vectors, but in order to visualize images with OpenCV and cv2.imshow, our images must be unsigned 8-bit integers in the range [0, 255] — Lines 81 and 82 take care of that operation for us.
The resulting component is then added to our list of images for visualization.
On Line 86 we build a montage of the top components.
We then display the mean eigenvector representation in similar fashion on Lines 90-94.
With visualization taken care of, let’s train our SVM on the eigenface representations:
# train a classifier on the eigenfaces representation
print("[INFO] training classifier...")
model = SVC(kernel="rbf", C=10.0, gamma=0.001, random_state=42)
model.fit(trainX, trainY)
# evaluate the model
print("[INFO] evaluating model...")
predictions = model.predict(pca.transform(testX))
print(classification_report(testY, predictions,
target_names=le.classes_))
Lines 98 and 99 initialize our SVM and train it.
We then use the model to make predictions on our testing data, taking care to project the testing data onto the eigenvalue subspace before making predictions.
This projection is a requirement. If you forget to perform the projection, one of two things will happen:
- Your code will error out (due to a dimensionality mismatch between the feature vectors and the SVM model)
- The SVM will return nonsense classifications (because the data the model was trained on was projected onto the eigenfaces representation)
Lines 104 and 105 then show a classification report, displaying the accuracy of our Eigenfaces recognition model.
The final step is to sample our testing data, make predictions on it, and display the results individually to our screen:
# generate a sample of testing data
idxs = np.random.choice(range(0, len(testY)), size=10, replace=False)
# loop over a sample of the testing data
for i in idxs:
# grab the predicted name and actual name
predName = le.inverse_transform([predictions[i]])[0]
actualName = le.classes_[testY[i]]
# grab the face image and resize it such that we can easily see
# it on our screen
face = np.dstack([origTest[i]] * 3)
face = imutils.resize(face, width=250)
# draw the predicted name and actual name on the image
cv2.putText(face, "pred: {}".format(predName), (5, 25),
cv2.FONT_HERSHEY_SIMPLEX, 0.8, (0, 255, 0), 2)
cv2.putText(face, "actual: {}".format(actualName), (5, 60),
cv2.FONT_HERSHEY_SIMPLEX, 0.8, (0, 0, 255), 2)
# display the predicted name and actual name
print("[INFO] prediction: {}, actual: {}".format(
predName, actualName))
# display the current face to our screen
cv2.imshow("Face", face)
cv2.waitKey(0)
We covered this code block in detail in last week’s guide on LBP face recognition so be sure to refer to it if you would like more details.
OpenCV Eigenfaces face recognition results
We are now ready to recognize faces using OpenCV and the Eigenfaces algorithm!
Start by accessing the “Downloads” section of this tutorial to retrieve the source code and CALTECH Faces dataset.
From there, open a terminal and execute the following command:
$ python eigenfaces.py --input caltech_faces --visualize 1
[INFO] loading face detector model...
[INFO] loading dataset...
[INFO] 397 images in dataset
[INFO] creating eigenfaces...
[INFO] computing eigenfaces took 0.1049 seconds
[INFO] training classifier...
[INFO] evaluating model...
precision recall f1-score support
abraham 1.00 1.00 1.00 5
allen 1.00 0.75 0.86 8
carmen 1.00 1.00 1.00 5
conrad 0.86 1.00 0.92 6
cynthia 1.00 1.00 1.00 5
darrell 1.00 1.00 1.00 5
frank 0.83 1.00 0.91 5
gloria 1.00 1.00 1.00 5
jacques 0.86 1.00 0.92 6
judy 1.00 1.00 1.00 5
julie 1.00 1.00 1.00 5
kenneth 1.00 1.00 1.00 6
mae 1.00 1.00 1.00 5
raymond 1.00 1.00 1.00 6
rick 1.00 1.00 1.00 6
sherry 1.00 0.83 0.91 6
tiffany 1.00 1.00 1.00 5
willie 1.00 1.00 1.00 6
accuracy 0.97 100
macro avg 0.97 0.98 0.97 100
weighted avg 0.97 0.97 0.97 100
Once our face images are loaded from disk, computing the Eigenfaces representation (i.e., eigenvalue decomposition) is quite fast, taking just over a tenth of a second.
Given the Eigenfaces, we then train our SVM. Evaluated on our testing set, we see we obtain ≈97% accuracy. Not too bad!
Let’s now move on to identifying faces in individual images:
[INFO] prediction: frank, actual: frank [INFO] prediction: abraham, actual: abraham [INFO] prediction: julie, actual: julie [INFO] prediction: tiffany, actual: tiffany [INFO] prediction: julie, actual: julie [INFO] prediction: mae, actual: mae [INFO] prediction: allen, actual: allen [INFO] prediction: mae, actual: mae [INFO] prediction: conrad, actual: conrad [INFO] prediction: darrell, actual: darrell

Figure 10 displays a montage of face recognition results using Eigenfaces. Notice how we’ve been able to correctly identify each of the faces.
Problems with Eigenfaces for face recognition
One of the biggest criticisms of the Eigenfaces algorithm is the strict facial alignment required when training and identifying faces:

Since we are operating at the pixel level, facial features such as eyes, nose, and mouth need to be aligned near perfectly for all images in our dataset. Not only is this a challenging task, it can be very hard to guarantee in real-world situations where conditions are less than ideal.
In our case, most faces in the CALTECH Faces dataset were captured from a frontal view with no viewpoint change, head tilt, etc. Due to this face we didn’t need to explicitly apply face alignment and everything worked out in our favor; however, it’s worth noting that this situation rarely happens in real-world conditions.
Last week we discussed Local Binary Patterns (LBPs) for face recognition. While LBPs can also suffer from not having adequate facial alignment, the results are far less pronounced and the approach is much more robust, since we split the face image into 7×7 cells and compute an LBP histogram for each cell
By quantifying the image into concatenated feature vectors, we are normally able to add additional accuracy to our face identifier — because of the added robustness, we normally use LBPs for face recognition rather than the original Eigenfaces algorithm.
What's next? I recommend PyImageSearch University.
30+ total classes • 39h 44m video • Last updated: 12/2021
★★★★★ 4.84 (128 Ratings) • 3,000+ Students Enrolled
I strongly believe that if you had the right teacher you could master computer vision and deep learning.
Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?
That’s not the case.
All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.
If you're serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.
Inside PyImageSearch University you'll find:
- ✓ 30+ courses on essential computer vision, deep learning, and OpenCV topics
- ✓ 30+ Certificates of Completion
- ✓ 39h 44m on-demand video
- ✓ Brand new courses released every month, ensuring you can keep up with state-of-the-art techniques
- ✓ Pre-configured Jupyter Notebooks in Google Colab
- ✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
- ✓ Access to centralized code repos for all 500+ tutorials on PyImageSearch
- ✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
- ✓ Access on mobile, laptop, desktop, etc.
Summary
In this tutorial, we discussed the Eigenfaces algorithm.
The first step in Eigenfaces is to supply a dataset of images with multiple images per person you want to recognize.
From there, we flatten each image into a vector and store them in a matrix. Principal Component Analysis is applied to this matrix, where we take the top N eigenvectors with the corresponding largest eigenvalue magnitude — these N eigenvectors are our eigenfaces.
For many machine learning algorithms, it’s often quite hard to visualize the results of a particular method. But for Eigenfaces, it’s actually quite easy! Each eigenface is simply a 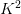
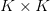
To identify a face, we first project the image onto the eigenface subspace, followed by utilizing a k-NN classifier with the Euclidean distance to find the nearest neighbor(s). These nearest neighbors are used to determine the overall identification. However, we can improve accuracy further by using more advanced machine learning algorithms, which is exactly what we did in this lesson.
Last week we discussed Local Binary Patterns (LBPs) for face recognition. In practice, this method tends to be a bit more robust than Eigenfaces, obtaining higher face recognition accuracy.
While neither method is as accurate as our modern deep learning face recognition models, it’s still important to understand from a historical perspective, and when applying deep learning models is just not computationally feasible.
To download the source code to this post (and be notified when future tutorials are published here on PyImageSearch), simply enter your email address in the form below!

Download the Source Code and FREE 17-page Resource Guide
Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you'll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!
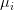 of each column in the matrix, giving us the average pixel intensity value for every (x, y)-coordinate in the image dataset.
of each column in the matrix, giving us the average pixel intensity value for every (x, y)-coordinate in the image dataset.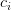 — this is called mean centering the data and is a required step when performing PCA.
— this is called mean centering the data and is a required step when performing PCA.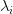 and eigenvectors
and eigenvectors 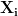 .
.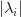 , largest to smallest.
, largest to smallest.

Comment section
Hey, Adrian Rosebrock here, author and creator of PyImageSearch. While I love hearing from readers, a couple years ago I made the tough decision to no longer offer 1:1 help over blog post comments.
At the time I was receiving 200+ emails per day and another 100+ blog post comments. I simply did not have the time to moderate and respond to them all, and the sheer volume of requests was taking a toll on me.
Instead, my goal is to do the most good for the computer vision, deep learning, and OpenCV community at large by focusing my time on authoring high-quality blog posts, tutorials, and books/courses.
If you need help learning computer vision and deep learning, I suggest you refer to my full catalog of books and courses — they have helped tens of thousands of developers, students, and researchers just like yourself learn Computer Vision, Deep Learning, and OpenCV.
Click here to browse my full catalog.